request@qapp.tech
RU
  • Products
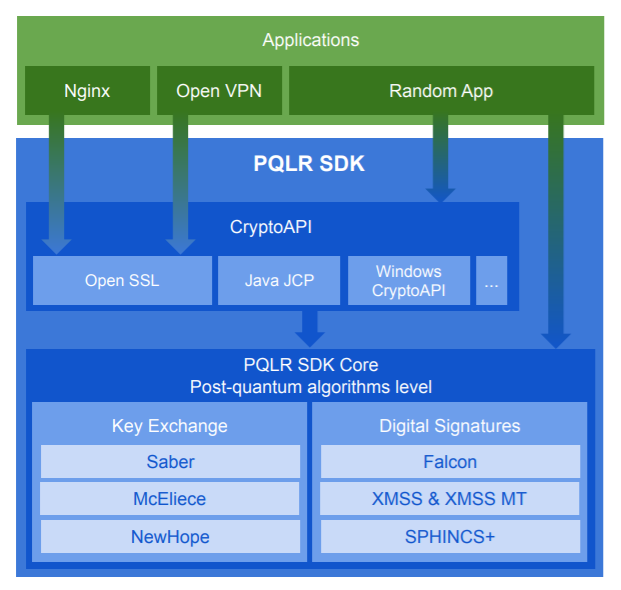
PQLR SDK
The QAPP team has developed a new generation of cryptographic algorithms that are resistant to attacks by quantum computers. These algorithms are compiled into the PQLR library and integrated into OpenSSLwhich makes it possible to use them in any application.

Algroithms benchmarks
TLS connection setup time benchmarks
Тechnical documents
Changelog
  • Cross-platform and portability
    Linux
    on x86-64, ARM v7

    Windows
    2012+, on x86-64

    Android
    ARM v7

    X86 ARM
  • Quantum-resistant algorithms
    NewHope
    Lattice-based

    Saber
    Module-LWR based key exchange

    SPHINCS+
    Hash-based

    McEliece
    Code-based

    Falcon
    Lattice-based

    XMSS и XMSS^MT
    Hash-based


  • Integration with OpenSSL
    OpenSSL
    1.0.2
    1.1.0
    1.1.1

    TLS
    1.3
    1.2

    KEM
    EDS
  • Reliability and security
    Theoretical validation
    Implementation testing
NewHope
NewHope is a key exchange protocol based on Ring-Learning-with-Errors (RingLWE).

All of the values below refer to a 256-bit key.
The total time is less than the sum because operations are performed on two remote sides.

Hardware test configuration:
Intel® Core™ i7-7700 CPU @ 3.60 GHz
Part 4, page 25
SABER
SABER is a key encapsulation algorithm based on a modular version of the error learning problem (Module-LWR).
Part 6, page 18
SPHINCS+
SPHINCS+ is a hash-based cryptographic scheme based on the cryptographic strength of a hash function. The scheme includes an algorithm for generating and verifying an electronic digital signature.

The algorithm has several sets of parameters that strongly affect the speed and size of signatures.
Minimum signature size, kB: 8
Maximum signature size, kB: 48

Hardware test configuration:
Intel® Core™ i7-7700 CPU @ 3.60 GHz
Part 9, page 42
McEliece
McEliece is a key encapsulation algorithm based on the decoding problem for a random linear code.
Part 6, page 35
Falcon
Falcon is a digital signature algorithm based on the problem of finding the shortest integer solution on NTRU lattices.
Part 2, page 10
XMSS
Hardware test configuration:
Intel® Core™ i7-7700 CPU @ 3.60 GHz
XMSS^MT
Par. 2.1, page 6
Hardware test configuration:
Intel® Core™ i7-7700 CPU @ 3.60 GHz
1. Expert evaluation by the mathematical and cryptographic community
Despite the fact that, in general, the question of the limits of the quantum computing capabilities remains open at the moment, the mathematical approaches underlying the post-quantum algorithms used in the PQLR library are one of the most deeply studied.
NewHope
Lattice-based

This algorithm is a very effective lattice-based algorithm of post-quantum cryptography in terms of security and speed, which is explained by the use of the mathematical properties of the rings that underlie it. The algorithm was considered one of the favorites of the NIST competition but did not make it to the final due to a number of minor comments on its algebraic structure.



SABER
Module-LWR based key exchange

One more variety of cryptographic algorithms for generating a common key based on the properties of rings, the SABER algorithm is a finalist in the NIST competition.
SPHINCS+, XMSS и XMSS^MT
Hash-based

Proofs of secrecy based on reduction techniques are among the most reliable in the cryptographic hash function algorithms used to construct SPHINCS and XMSS. The SPHINCS+ algorithm is an alternative finalist for the NIST competition. The XMSS algorithm is standardized by the IETF.





Falcon
Lattice-based digital signature

One of the most effective post-quantum digital signature schemes based on NTRU lattices, the Falcon scheme is a finalist in the NIST competition.
McEliece
Code-based

The history of cryptanalysis of the McEliece system goes back more than 40 years. In addition, an adequate choice of the error-correcting code family used in the system guarantees its strength. The McEliece algorithm is a finalist in the NIST competition.
2. Complementarity of algorithms from the point of view of mathematical approaches
The choice of cryptographic algorithms implemented in the library is based on the necessity of using different classes of complex mathematical problems that are resistant to analysis using a quantum computer. These include the following problems:
Shortest vector problem
Decoding full linear codes
Searching for the second preimage/collision/reversal of the hash function
Solving non-linear equations over a finite field
Using a set of cryptographic algorithms based on fundamentally different mathematical tasks allows you to provide an additional level of security for information systems if any of these algorithms is compromised.